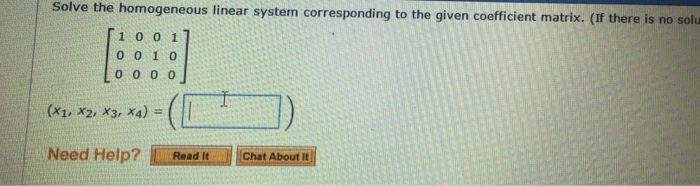
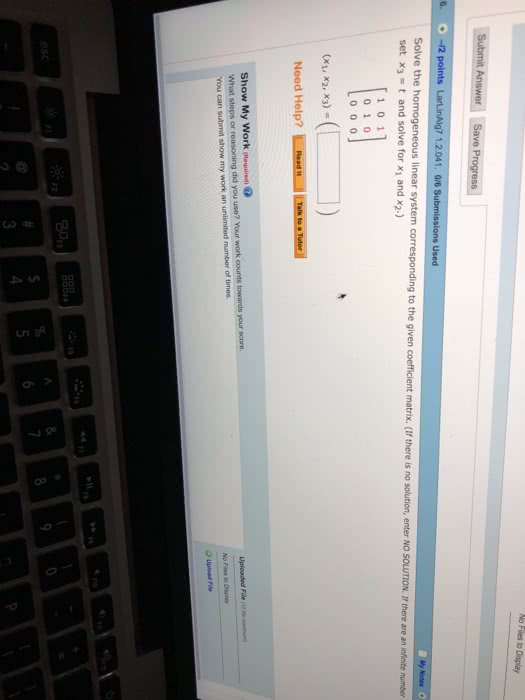
Solve The Homogeneous Linear System Corresponding To The Given Coefficient Matrix
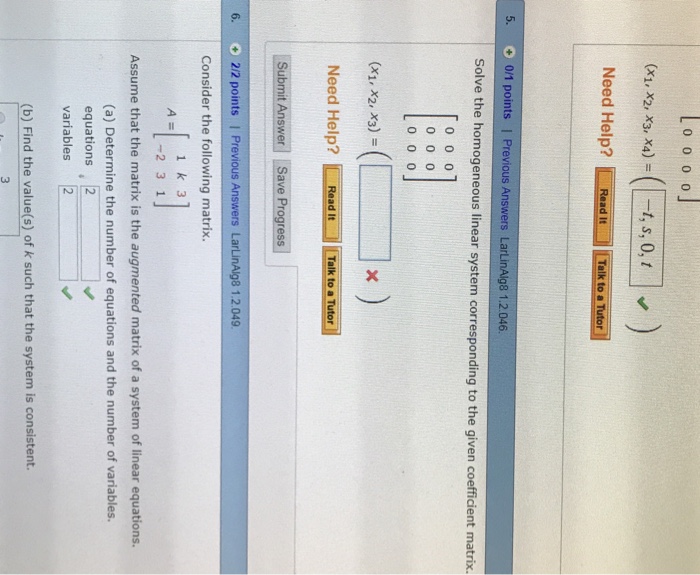
Solve the homogeneous linear system corresponding to the given coefficient matrix. Homogeneous System solve the homogeneous linear system corresponding to the given coefficient matrix. Solve the homogeneous linear system corresponding to the given coefficient matrix. X1 -t x2 s x3 0 x4 t.
One method for finding the solution space of a homogeneous system is to first use Gaussian elimination as demonstrated in Example A35 in order to factor the coefficient matrix of the system. The final part of the question which is what this post is about has asked me to find the solution set of the corresponding homogeneous system of linear equations. For other fundamental matrices the matrix inverse is needed as well.
1 0 0 1 0 0 1 0 0 0 0 0. A homogeneous system always has vec 0 as a particular solution and the second theorem applies to homogeneous systems by taking vec pvec 0. D A homogeneous linear system in n unknowns whose corresponding augmented matrix has a reduced row echelon form with r leading 1s has n r free variables.
A system of linear equations AX B can be solved by reducing the augmented matrix of the system to row canonical form by elementary row operations. 1 0 0 0 0 1 1 0. If there is no solution enter NO SOLUTION.
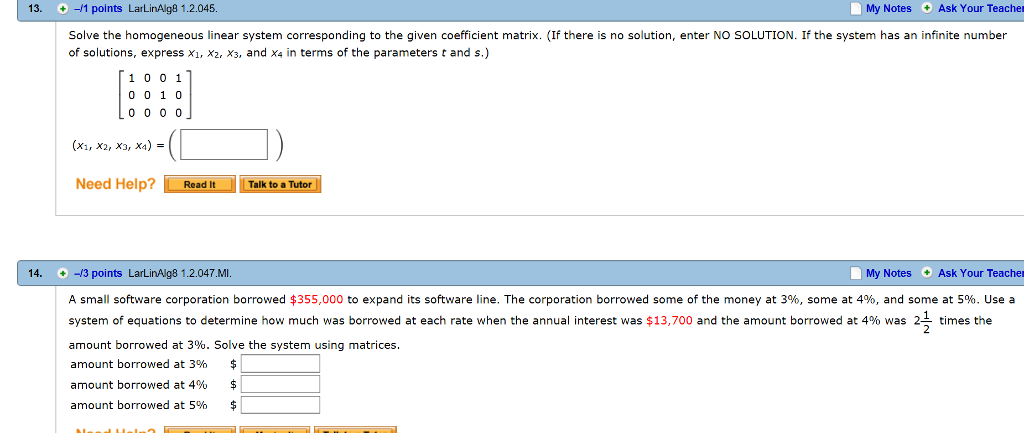
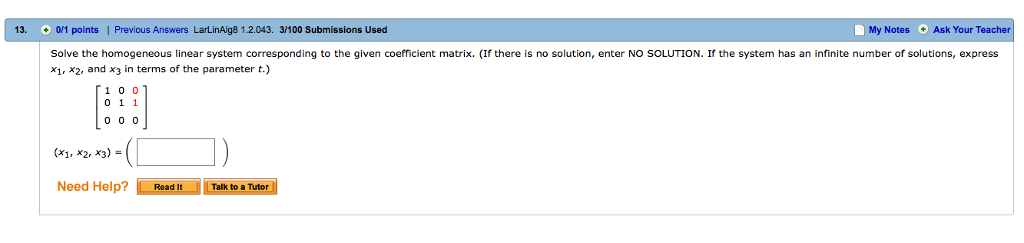
If there is no solution enter NO SOLUTION. Homogeneous system In Exercises 4346 solve the homogeneous linear system corresponding to the given coefficient matrix. Ax 0 Solution Sets of Inhomogeneous Systems Another Perspective on Lines and Planes Solving Homogeneous Systems Youve Won.
Transform the coefficient matrix to the row echelon form. If the system has an infinite number of solutions set x 4 t and x 2 s and solve for x 1 and x 3 in terms of t and s. Thus our final answer is.
Moreover given any homogenous system of m linear equations in n unknowns there exist solutions ie vectors v 1v kin Rn such that every solution to the system is a linear combination of v 1v k. If there is no solution enter NO SOLUTION.
Homogeneous system In Exercises 4346 solve the homogeneous linear system corresponding to the given coefficient matrix.
Find the eigenvalues and eigenvector of UtransposeU e_vals e_vecs nplinalgeignpdotUT U extract the eigenvector column associated with the minimum eigenvalue return e_vecs npargmine_vals. X1 0 x2 -t x3 t 44. Import numpy as np def solutionU. Formed by appending the constant vector bs to the right of the coefficient matrix. If there is no solution enter NO SOLUTION. For other fundamental matrices the matrix inverse is needed as well. If there is no solution enter NO SOLUTION. Note that for a given system the vectors vec p and vec v_i are not unique. Solving a system of linear equations by reducing the augmented matrix of the system to row canonical form.
Recall that a linear equation is homogeneous if the right-hand side or constant is zero The term homogeneous implies all terms are of the same format In a homogeneous linear equation all terms are of the form a coefficient times an unknown. 1 0 0 1 0 0 1 0 0 0 0 0. That is ρ A ρ A B. Example Row one gives x 1 2x 3 3x 5 row two gives x 2 x 3 6x 6 and row three gives x 4 4x 5 5x 6. Solving systems of linear equations. X1 -t x2 s x3 0 x4 t. Setting x 2 c 1 and x 3 c 2 we obtain the following homogeneous linear system.








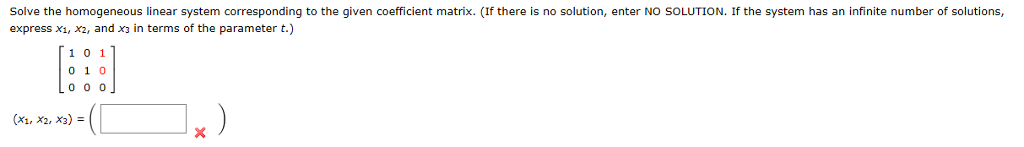









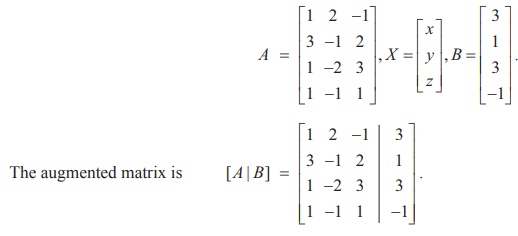


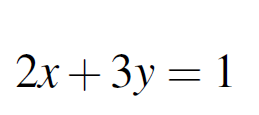







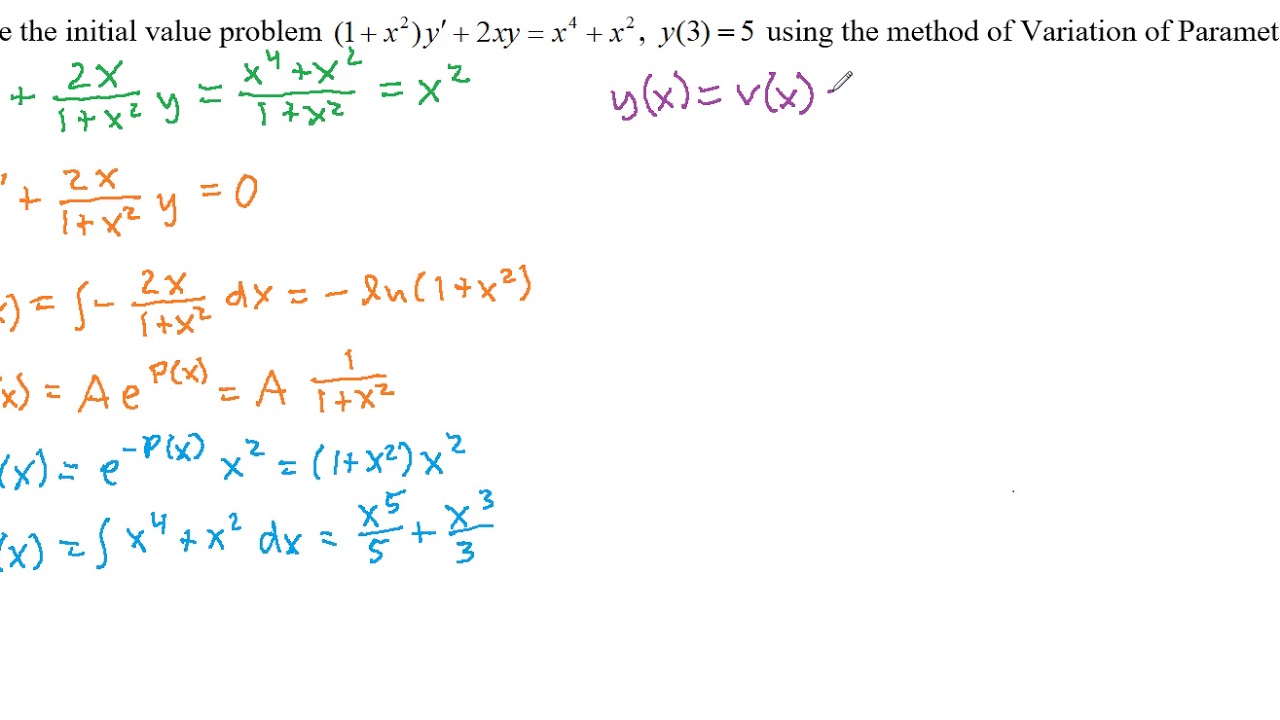

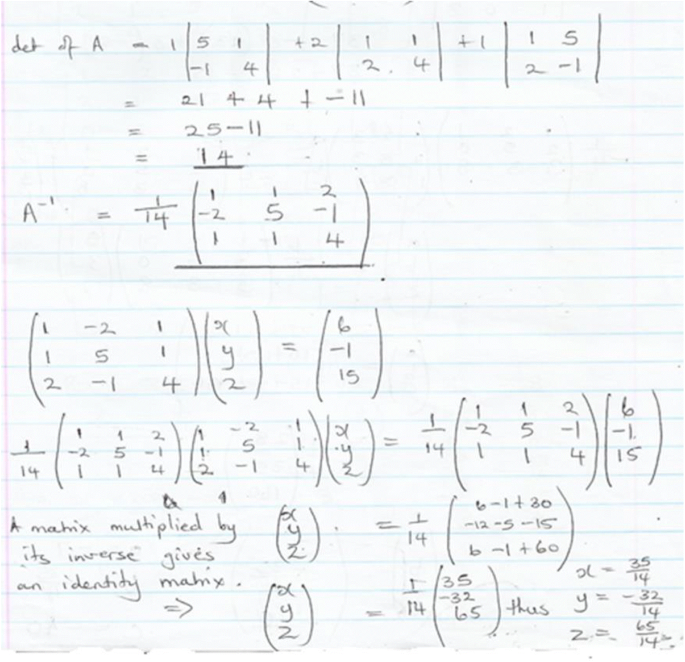
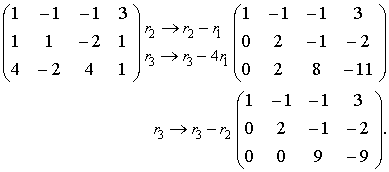



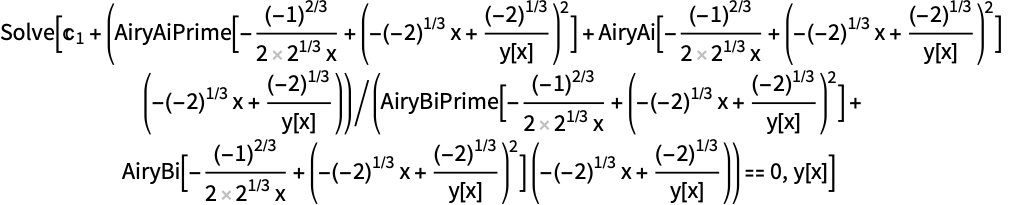


Post a Comment for "Solve The Homogeneous Linear System Corresponding To The Given Coefficient Matrix"